«عدد چیه؟ از کجا اومده؟ میشه به یه حالت مجرد تعمیمش داد و یا حداقل تعریفی مجرد ازش ارائه داد؟ مگه فقط اعداد مثبت زیر رادیکال نمیرفتن؟ پس 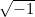 قضیهش چیه؟». اینها نمونه سوالاتی هستند که در مورد اعداد به ذهن میرسند. در این نوشته، قرار است تا با قرائتی طنزگونه و تخیلی، با چگونگی تکامل اعداد آشنا شویم. مطالب این نوشته، «فقط» برداشتها و خیالبافیهای ذهنی نویسنده است و لزوما در واقعیت وجود نداشتهاند و یا وجود ندارند.
قضیهش چیه؟». اینها نمونه سوالاتی هستند که در مورد اعداد به ذهن میرسند. در این نوشته، قرار است تا با قرائتی طنزگونه و تخیلی، با چگونگی تکامل اعداد آشنا شویم. مطالب این نوشته، «فقط» برداشتها و خیالبافیهای ذهنی نویسنده است و لزوما در واقعیت وجود نداشتهاند و یا وجود ندارند.
مفهوم عدد ۱، ابتداییترین مفهومی است که میتوان برای اعداد تصور کرد. به هر تصوری از فردیت هر چیز، ۱ میگوییم. یک که آن را با نماد ۱ نشان میدهیم، شاید نماد یک چوب باشد که در داد و ستدها مورد استفاده قرار گرفته میشده است. واضح است که با این نگاه، میشود عدد ۲ را، ابداع بشر برای ۱ چوب و ۱ چوب دانست، یعنی چیزی مثل این: ||، و عدد ۳، یک چوب و یک چوب و یک چوب: ||| و قس علی هذا. در تاریخ آمده است که با توجه به توانایی حمل چوب بشر، در هر دوره، برای تعداد چوبها محدودیت وجود داشته است، برای مثال در همان دورهی آدم و حوا، فقط عبارات «۱ چوب، ۱ چوب و ۱ چوب، ۱ چوب و ۱ چوب و ۱ چوب» را داشتیم و برای مقادیر بیشتر از آن، از عبارت «خیلی» استفاده میشده است. تدریجا با پیشرفت بشر و همراهی توامان نیاز به اعداد بزرگتر و توانایی حمل چوب بیشتر، عبارت «خیلی»، جایگزین اعداد بزرگتر و بزرگتری میشده است و به همین جهت، کمکم کاربرد خودش را در محاورات روزمره از دست میدهد.
به این دسته از اعداد که آنها را به صورت معمول با ۱، ۲، ۳، ۴، ۵، ۶ و … نشان میدهیم، اعداد طبیعی میگوییم. شاید چون با استفاده از ابتداییترین عناصر طبیعت، میتوان آنها را ساخت.
شاید بتوان گفت که بزرگترین ابداع و اختراع بشر، همین صفر بوده است. امروز اگه شما به هر جا نگاه کنید، تنها عددی که در همه جا هست، همین صفر است، حتی جایی که عدد صفر نباشد، باز صفر تا عدد صفر رو میشود دید!
با این نیاز، بشر اعداد طبیعی منفی را آفرید. اعدادی که قرار بود نقصان چیزی را نشان دهند، اعداد طبیعی منفی، همان اعداد طبیعی بودند، ولی یک خط تیره در کنار خود، برای نشان دادن نقص داشتند. به مجموعهی اعدادی مثل
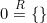 ، یک نماد مجموعهای است که یک عضو دارد: «مجموعهی تهی»، یعنی
، یک نماد مجموعهای است که یک عضو دارد: «مجموعهی تهی»، یعنی  . به همین صورت، ۲، نماد مجموعهای است که یک عنصر ۰ دارد و یک عنصر ۱:
. به همین صورت، ۲، نماد مجموعهای است که یک عنصر ۰ دارد و یک عنصر ۱: 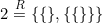 و ….
و ….
اینگونه اعداد گویا ابداع شدند. اعداد گویا، با تقسیم دو عدد صحیح بر هم به وجود میآیند. برای مثال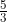 و یا
و یا 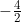 . تا سالها این دسته از اعداد، تمام نیاز بشر را پوشش میدادند و به نظر میرسید که که تمام آنچه بشر میخواسته، همین است!
. تا سالها این دسته از اعداد، تمام نیاز بشر را پوشش میدادند و به نظر میرسید که که تمام آنچه بشر میخواسته، همین است!
قسم به تقدس ناتمام
با ابداع اعداد گویا و ثبات نسبی آن در پاسخگویی به نیازهای بشر و ماندگاری آن در طی صدها سال، کمکم مردم برای این دسته از اعداد یک نوع تقدس را قائل شدند. در این بین نقش علما و دانشمندان آن زمان نیز، پررنگ و روشن است. اعداد برای یونان باستان، در حکم هوا برای تنفس بود و آنها تصور میکردند که هر چیزی را میتوان با این دسته از اعداد، تشریح کرد و اگر هم که بعضی از موارد را نمیتوانستند تشریح کنند، تقصیر را به گردن جهل خودشان میانداختند و نه اعداد، تا جایی که یکی از شعرای آن زمان میگوید: «اعداد به ذات خود ندارند عیبی / هر عیب که هست در ریاضدانی۳ ماست.». وضع در یونان به همین منوال پیش میرفت و پایههای مقدس و بیعیب انگاشتن اعداد، قوی و قویتر میشد. در همین دوران، شخصی که از رابطهی فیثاغورث در مثلثها ( ) آگاه بود، سوالی را مطرح کرد: «طول وتر مثلث قائمالزاویهی متساویالساقینی به طول ۱، چقدر است؟». این مسئله به این صورت نیز قابل بیان است: «عدد
) آگاه بود، سوالی را مطرح کرد: «طول وتر مثلث قائمالزاویهی متساویالساقینی به طول ۱، چقدر است؟». این مسئله به این صورت نیز قابل بیان است: «عدد  را چنان بیابید که
را چنان بیابید که  .».
.».
این مسئله ابتدا در بین علمای یونان مطرح شد، در بین اعداد گویا ظاهرا عددی نبود که بتواند در این مسئله صدق کند. تصور ناقص بودن اعداد گویا، به عنوان بزرگترین مجموعهی اعداد شناخته شده در آن زمان، لرزه بر اندام دانشمندان انداخته بود: «با این باور مقدس چه کنیم؟». ابتدا قرار شد، این مسئله در بین علما باقی مانده و از چشم مردم دور بماند، اما در نهایت، این مسئله به مردم راه پیدا کرد و باور به تقدس اعداد، رو به افول نهاد.

تعریف میشود. با این تعریف، نقطهای که در معادلهی  صدق میکند را
صدق میکند را 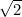 نامیدند، به این دلیل که این عدد، دارای توجیهی گویا نیست، آنرا گنگ نام نهادند!
نامیدند، به این دلیل که این عدد، دارای توجیهی گویا نیست، آنرا گنگ نام نهادند!
از آنجا که به وضوح، یک خط هیچ سوراخی ندارد، مجموعهی نقاط یک خط را نهایت اعداد فرض کردند و آنرا حقیقت اعداد نامیدند: «اعداد حقیقی».
 را چنان بیابید که معادلهی
را چنان بیابید که معادلهی  جواب داشته باشد.». این مسئله را به این صورت نیز میتوان بیان کرد که «عدد
جواب داشته باشد.». این مسئله را به این صورت نیز میتوان بیان کرد که «عدد  را چنان بیابید که
را چنان بیابید که 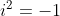 .». اعداد حقیقی از همانجا که قدرت یافته بودند، ضربه خوردند. تلاش برای یافتن جواب این مسئله ناتمام ماند و از طرفی، کاربردهای متنوعی نیز از حوزههای مختلف، به یافتن جوابی برای مسئلهی مذکور منتج میشدند.
.». اعداد حقیقی از همانجا که قدرت یافته بودند، ضربه خوردند. تلاش برای یافتن جواب این مسئله ناتمام ماند و از طرفی، کاربردهای متنوعی نیز از حوزههای مختلف، به یافتن جوابی برای مسئلهی مذکور منتج میشدند.
«چه باید کرد؟»، تمام آنچه دیده میشود، همان حقیقی بود، تمام حقیقتی که ما میدیدیم. سرانجام همان کاری انجام شد که برای ساخت اعداد حقیقی انجام شد، عدد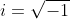 آن عددی تعریف شد که
آن عددی تعریف شد که 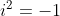 . اما این عدد با ساخت ما از اعداد حقیقی که فاصلهی نقطه از نقطهی صفر، بود در تضاد و مشکل بود: «فاصلهی منفی چیست؟ و اصولا چگونه توان دوم یک عدد که همیشه نامنفی است، منفی میشود؟». این بیشتر به یک سوال تخیلی میماند و با این توجیه، دستهی جدید اعداد ساخته شده با
. اما این عدد با ساخت ما از اعداد حقیقی که فاصلهی نقطه از نقطهی صفر، بود در تضاد و مشکل بود: «فاصلهی منفی چیست؟ و اصولا چگونه توان دوم یک عدد که همیشه نامنفی است، منفی میشود؟». این بیشتر به یک سوال تخیلی میماند و با این توجیه، دستهی جدید اعداد ساخته شده با  را اعداد موهومی نامیدند: «چیزی که در وهم است و در واقعیت نمیتوان آنرا دید.».
را اعداد موهومی نامیدند: «چیزی که در وهم است و در واقعیت نمیتوان آنرا دید.».
اکنون بشر به نقطهای رسیده است که مجموعهی اعداد به صورت به عنوان مخلوطی از اعداد حقیقی و موهومی را اعداد مختلط میخواند و میتواند تمام نیازهایش به اعداد را با این مجموعه پاسخ گوید.
به عنوان مخلوطی از اعداد حقیقی و موهومی را اعداد مختلط میخواند و میتواند تمام نیازهایش به اعداد را با این مجموعه پاسخ گوید.
۱. نماد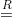 برای اختصار «نماینده» به کار برده شده است، از Representative.
برای اختصار «نماینده» به کار برده شده است، از Representative.
۲. مهم نیست که در یک مجموعه چه باشد! اگر تعداد اعضای دو مجموعه، با هم برابر باشند، میتوان با یک چوب جادویی، یک مجموعه را به دیگری تبدیل کرد! مهم فقط همین نکته است که اعضای دو مجموعه برابر باشند (در غیراینصورت، برای تبدیل معکوس مجموعه، نمیدانیم عضو اضافه را به چه چیز تبدیل کنیم؟!). همچنین تکرار در یک مجموعه اثر ندارد، برای مثال اگر من در جواب تماس تلفنی مادرم که پرسیده «کی اونجاس؟»، بگویم: «من» و یا بگویم «من و من و من و من»، هیچ تفاوتی ندارد (هر چند در حالت دوم، مطمئن میشود که امیدی به بهبود پسرش نیست! :دی.».
۳. همان ریاضیدان که ظاهرا شاعر مذکور به خاطر وزن شعر، دمش را زده تا به کاری که به وی مربوط نیست، دخالت نکند.
به یاد اولین دیدار
در بعضی داستانها آمده است که اولین بار که آدم، حوا را دید، به خودش لرزید، خواست به وی ابراز علاقه کند، سنگ زد به درخت نارگیل و با دستش نارگیلی برداشت و به سمت حوا رفت و به حوا نارگیل را تعارف کرد. حوا گفت: «فقط یک نارگیل؟» و اینجا زندگی عاشقانه این دو نوگل هستی آغاز شد.مفهوم عدد ۱، ابتداییترین مفهومی است که میتوان برای اعداد تصور کرد. به هر تصوری از فردیت هر چیز، ۱ میگوییم. یک که آن را با نماد ۱ نشان میدهیم، شاید نماد یک چوب باشد که در داد و ستدها مورد استفاده قرار گرفته میشده است. واضح است که با این نگاه، میشود عدد ۲ را، ابداع بشر برای ۱ چوب و ۱ چوب دانست، یعنی چیزی مثل این: ||، و عدد ۳، یک چوب و یک چوب و یک چوب: ||| و قس علی هذا. در تاریخ آمده است که با توجه به توانایی حمل چوب بشر، در هر دوره، برای تعداد چوبها محدودیت وجود داشته است، برای مثال در همان دورهی آدم و حوا، فقط عبارات «۱ چوب، ۱ چوب و ۱ چوب، ۱ چوب و ۱ چوب و ۱ چوب» را داشتیم و برای مقادیر بیشتر از آن، از عبارت «خیلی» استفاده میشده است. تدریجا با پیشرفت بشر و همراهی توامان نیاز به اعداد بزرگتر و توانایی حمل چوب بیشتر، عبارت «خیلی»، جایگزین اعداد بزرگتر و بزرگتری میشده است و به همین جهت، کمکم کاربرد خودش را در محاورات روزمره از دست میدهد.
به این دسته از اعداد که آنها را به صورت معمول با ۱، ۲، ۳، ۴، ۵، ۶ و … نشان میدهیم، اعداد طبیعی میگوییم. شاید چون با استفاده از ابتداییترین عناصر طبیعت، میتوان آنها را ساخت.
هیچی!
میگویند همان اوایل ازدواج آدم و حوا بود که برای خرید نان، به نانوایی رفت، آدم گفت: «آقا ۳ چوب نون بده!» و جواب شنید: «۳ چوب!!!، مگه چقد پول داری؟» و آدم جواب داد: «هیچی!». نانوا که برآشفته شده بود، گفت: «هیچی؟ هیچی چیه؟» و اینجا مفهوم صفر ابداع شد.شاید بتوان گفت که بزرگترین ابداع و اختراع بشر، همین صفر بوده است. امروز اگه شما به هر جا نگاه کنید، تنها عددی که در همه جا هست، همین صفر است، حتی جایی که عدد صفر نباشد، باز صفر تا عدد صفر رو میشود دید!
جاده به جز جدایی، هیچی به من نداده
عالم و آدم، همه با هم خوب بودند و تمام نیازشان به اعداد را، اعداد طبیعی با «خیلی» معادل ۲۰ امروز ما رفع میکرد که یک روز، حاوا، نوهی حوا، از این نکته مطلع شده که زنِ بردارِ شوهرش، ۵تا قاشق چنگال بیشتر از وی دارد! خلاص! تقاضای طلاق داد و قرار شد، آدام -شوهرش، نوهی آدم- مهریهی وی، که از قرار معلوم ۲خیلی نارگیل بود را بپردازد و وی را از شر این زندگی نکبتبار خلاص کند. آدام، توانست با هر زر و زور، ۱خیلی و ۱۵ نارگیل مهریه را بپردازد، اما موقعی که از قاضی پرسید که «من ۱خیلی و ۱۵ نارگیل را از ۲خیلی نارگیل پرداختهام، چقدر مانده است؟»، مشکلی به وجود آمد، نقص را با چه باید نشان میدادند؟ در اینجا قاضی که از قضا عرب بود، ابتکاری به خرج داد و گفت: «۵ منفیه»، یعنی شما ۵ بار بیا آن نارگیل را در جایی که من هستم، پرداخت کن (انصافا خلاقیتم عالی بود. :دی) تا به صفر برسی! و همه گفتند: «صحیح است! صحیح است!».با این نیاز، بشر اعداد طبیعی منفی را آفرید. اعدادی که قرار بود نقصان چیزی را نشان دهند، اعداد طبیعی منفی، همان اعداد طبیعی بودند، ولی یک خط تیره در کنار خود، برای نشان دادن نقص داشتند. به مجموعهی اعدادی مثل
...،-۵،-۴،-۳،-۲،-۱،۰،۱،۲،۳،۴،۵،…
اعداد صحیح میگوییم.تکامل
در مسیر تکامل اعداد، برای حل مشکل نوشتن، رقمها به وجود آمدند. جدول زیر، مسیر تکامل رقمهای ۰ تا ۹ را نشان میدهد. در حالت مجرد، اعداد را اینگونه میتوان تعبیر کرد: نماد صفر، نماینده۱ مجموعهای۲ است که تهی است (یعنی هیچ عضوی ندارد):۳خیلیخیلیخیلیییی
در تاریخ آمده است که روزی در دوران آدم و حوا، دیوان قضای کشوری، پرده از فساد مالیای را برداشت که نه برای آن دیوان قابل درک بود و نه برای مردم. برای مثال، وقتی سخنگوی دیوان قضا میخواست مقدار اختلاس کشفشده را اعلام کند، گفت: «۳خیلیخیلیخیلیییی» و این ییی آخرش را اینقد کشید که نفس کم آورد و جان به جانآفرین تسلیم کرد. با اعلام این فساد، از آنجا که عدالت در آن دیار حکمفرما بود، دادگاهی برای رسیدگی میزان اختلاس کشف شد و از آنجا که نیاز بود هر کس به اندازهی سهمش مجازات شود، قرار شد بررسی شود که هر کس چه مقدار از این ۳خیلیخیلیخیلیییی را قرض بلاعوض گرفته است. پس از بررسیها، چون تعداد افراد زیاد بود و قاضی باید حکم را قرائت میکرد، قرار شد اول مقداری که طرف خورده است را بگوید و بعد مقدار کل اختلاس را، مثلا بگوید، ۵خیلی، ۳خیلیخیلیخیلییی، اما از آنجا که با خواندن هرکدام، تأملی میکرد و یا نفسش به خاطر بزرگی اعداد میگرفت، آخر هر جمله، ناخواسته، یک «م» اضافه میشد (همان اسمایلی نفسنفس زدن خودمان، توضیح از بندهی نگارنده.) و عبارت مذکور به ۵خیلی، ۳خیلیخیلیخیلییییم تبدیل میشد و اینگونه بود که همه گفتند! ایول، چقد شیوهی بیان مقدار اختلاس هر فرد توسط قاضی، گویا بود!اینگونه اعداد گویا ابداع شدند. اعداد گویا، با تقسیم دو عدد صحیح بر هم به وجود میآیند. برای مثال
قسم به تقدس ناتمام
با ابداع اعداد گویا و ثبات نسبی آن در پاسخگویی به نیازهای بشر و ماندگاری آن در طی صدها سال، کمکم مردم برای این دسته از اعداد یک نوع تقدس را قائل شدند. در این بین نقش علما و دانشمندان آن زمان نیز، پررنگ و روشن است. اعداد برای یونان باستان، در حکم هوا برای تنفس بود و آنها تصور میکردند که هر چیزی را میتوان با این دسته از اعداد، تشریح کرد و اگر هم که بعضی از موارد را نمیتوانستند تشریح کنند، تقصیر را به گردن جهل خودشان میانداختند و نه اعداد، تا جایی که یکی از شعرای آن زمان میگوید: «اعداد به ذات خود ندارند عیبی / هر عیب که هست در ریاضدانی۳ ماست.». وضع در یونان به همین منوال پیش میرفت و پایههای مقدس و بیعیب انگاشتن اعداد، قوی و قویتر میشد. در همین دوران، شخصی که از رابطهی فیثاغورث در مثلثها (این مسئله ابتدا در بین علمای یونان مطرح شد، در بین اعداد گویا ظاهرا عددی نبود که بتواند در این مسئله صدق کند. تصور ناقص بودن اعداد گویا، به عنوان بزرگترین مجموعهی اعداد شناخته شده در آن زمان، لرزه بر اندام دانشمندان انداخته بود: «با این باور مقدس چه کنیم؟». ابتدا قرار شد، این مسئله در بین علما باقی مانده و از چشم مردم دور بماند، اما در نهایت، این مسئله به مردم راه پیدا کرد و باور به تقدس اعداد، رو به افول نهاد.
حقیقت: آنچه که میبینید!
با نمایان شدن نقصان اعداد گویا، باز جنب و جوشی در بین ریاضیدانان، برای ساختن یک مجموعه عدد برای تمام نیازها به وجود آمد. این تلاشها در نهایت به ساختن مجموعهی اعداد حقیقی منجر شد. اعداد حقیقی، حاصل نگاه به یک خط راست به صورت پیوسته بودند: «فاصلهی هر نقطه روی خط از صفر، نمایشگر یک عدد است.». اما فاصله چه بود؟ فاصله دو نقطه از هم، به صورتاز آنجا که به وضوح، یک خط هیچ سوراخی ندارد، مجموعهی نقاط یک خط را نهایت اعداد فرض کردند و آنرا حقیقت اعداد نامیدند: «اعداد حقیقی».
باور ناتمام
با ابداع (و یا اکتشاف) اعداد حقیقی، در تمامی علوم، زمینههای تحقیقات جدیدی باز شد، اما جان کلام اکثر آنها، یافتن ریشهی معادلات بود. اعداد حقیقی به خوبی جوابگوی این نیاز بودند و تا سالها، این اعداد میتوانستند جواب هر معادلهای که در یک کاربرد یافت میشود را از بین خود انتخاب و نشان دهند. اما باور به تمامیت اعداد حقیقی و کامل بودن آن برای تمام نیازها نیز، دیری نپائید که دچار چالش دیگری شد. حقیقت، تمام آنچه که ما میدیدیم نبود! سوال جدیدی مطرح شد: «عدد«چه باید کرد؟»، تمام آنچه دیده میشود، همان حقیقی بود، تمام حقیقتی که ما میدیدیم. سرانجام همان کاری انجام شد که برای ساخت اعداد حقیقی انجام شد، عدد
اکنون بشر به نقطهای رسیده است که مجموعهی اعداد به صورت
بازگشت ماتریکس
آیا مجموعهی اعداد مختلط، آخرین مجموعهی عددی است که بشر ابداع کرده است؟ آیا تمام حقیقت این است که ما اکنون با مخلوطی از حقیقت و وهم میبینیم؟ آیا بشر به نقطهای خواهد رسید که باز نیاز به داشتن مجموعهای کاملتر از اعداد مختلط کند؟۱. نماد
۲. مهم نیست که در یک مجموعه چه باشد! اگر تعداد اعضای دو مجموعه، با هم برابر باشند، میتوان با یک چوب جادویی، یک مجموعه را به دیگری تبدیل کرد! مهم فقط همین نکته است که اعضای دو مجموعه برابر باشند (در غیراینصورت، برای تبدیل معکوس مجموعه، نمیدانیم عضو اضافه را به چه چیز تبدیل کنیم؟!). همچنین تکرار در یک مجموعه اثر ندارد، برای مثال اگر من در جواب تماس تلفنی مادرم که پرسیده «کی اونجاس؟»، بگویم: «من» و یا بگویم «من و من و من و من»، هیچ تفاوتی ندارد (هر چند در حالت دوم، مطمئن میشود که امیدی به بهبود پسرش نیست! :دی.».
۳. همان ریاضیدان که ظاهرا شاعر مذکور به خاطر وزن شعر، دمش را زده تا به کاری که به وی مربوط نیست، دخالت نکند.




مطلب جالبی بود